Pfeilhöhenberechnung bei Übergangsbögen

[jgifhorn]

Hallo an alle,

Ich muss gestehen, dass ich ein kleines bißchen verzweifelt bin. Ich suche nun schon überall nach Formeln, die mir helfen, die Pfeilhöhen von Übergangsbögen (Bloss, Klotoide und S) zu berechnen. Alles was ich bisher finden konnte, waren die Pfeilhöhen für Kurven mit konstantem Radius.

Echt jetzt... Darüber findet man haufenweise Literatur. Wie baut man eine Trasse und wie legt man die Höchstgeschwindigkeit fest. Aber zu den Pfeilhöhen gibt es wirklich wenig.

Besondere Schwierigkeit besteht darin, dass Pfeilhöhen auf Sehnen berechnet werden, die zwischen zwei Fixpunkten liegen und diese sind nicht unbedingt am Anfang oder am Ende eines Übergangsbogens.

Gibt es hier vielleicht jemanden, der mir helfen kann oder mir zumindest ein Nachschlagewerk empfehlen kann, dass sich nicht nur mit der Entwicklung einer Gleistrasse beschäftigt, sondern auch mit deren Vermessung?

 

[MephisTTo]

Erst mal ein freundliches Hallo!

Unser Spezie dafür ist in China letztmalig gesichtet worden...

Mit dem Begriff "Pfeilhöhen " kann ich selbst im Moment wenig anfangen. Meinst Du die Neigung der Gleise in den Kurven?
Kannst Du das bitte näher erläutern?

Wenn`s ums Einpassen von Weichen geht , dann ev. Hartmann, " Reichsbahnweichen und Reichsbahnbogenweichen".
Als Link vielleicht die Oberbauvorschriften der DRG.

 

[tommy]

Könnte Dir Dieses helfen...?

mfg tommy

 

[DanNHG]

http://www.gleisbau-welt.de/site/vermessung/pfeilhoehenmessung.htm

Der Link hilft

 

[jgifhorn]

Hey... ich danke Euch schon mal sehr.

Eins noch vorweg, es geht um Schienenvermessung. Mit meiner Firma versuchen wir eine entsprechende Software zu entwickeln.

Pfeilhöhen sind die Höhen, die man braucht, um zu überprüfen, ob die Schienen dort liegen wo sie sollen. Man spannt zwischen zwei Punkten eine Sehne und bestimmt dann damit die Entferng zur Kurve. Dass macht man dann alle 5m und damit kann man dann eine Kurve definieren. Die Länge von der Sehne zur Kurve nennt man Pfeilhöhe. (Auch wenn ich den Begriff Fallhöhe passender finden würde)
Diese Pfeilhöhen für Kurven (mit konstanten Radius) herauszufinden, ist sehr leicht. Da gibt es wunderschöne Annäherungsrechnungen, wie der Link von DanNHG schön zeigt. (@ DanNHG: Vielen Dank dafür, aber leider wird dort nur die Bestimmung von Pfeilhöhen bei Kurven (mit konstanten Radius) beschrieben. Übergangsbögen leider nicht.)

Das Problem ist nun, dass diese Sehnen nicht nur dann aufgespannt werden, wenn man eine reine Kurve vorliegt, sondern auf bei Übergangsbögen. Dass heißt ich brauche eine Methode, wie ich diese Höhen zu einer definierten Sehne auch bei Übergangsbögen berechnen kann. Und was es nun noch ein bißchen schlimmer macht, ist dass zwischen diesen Punkten, zwischen denen die Sehne aufgespannt wird auch Mischformen liegen können. Also ein halber Übergangsbogen und dann ein Teil einer Kurve oder eine Gerade.

@ tommy: Nein... so richtig hilft es nicht. Es beschreibt, wie ein Übergangsbogen aufgebaut ist, aber die Höhe zu einer definierten Sehne kann ich davon leider nicht ableiten.

 

[DanNHG]

Ich messe bei mir auf Arbeit die Pfeilhöhen immer direkt mit unseren Wuppertaler Latten,übertrage sie dann ins Diagramm

Nach ÜE ist dann schluss mit messen,also wird der Übergangsbogen mitgemessen

 

[jgifhorn]

Tja... aber unser Kunde will es nun mal elektronisch haben. Und die Bahn eigentlich auch. Damit es schön genau ist.

 

[ptlbahn]

http://www.gleisbau-welt.de/site/vermessung/pfeilhoehenmessung.htm

Der Link hilft

Bitte um Hilfe!
Irgendwie ist mir das Ergebnis der Formel unlogisch!
Hf=a*b/2r
wenn ich als Sehne 20 einsetze, a=b annehme und als Radius 10 ansetze bekomme ich 5 heraus.
Ich habe aber mal gelernt, das der Durchmesser die größte Sehne ist. Demnach müsste also das Ergebnis für meine Angenommenen Werte auf gehen, und Hf= r heraus kommen, und nicht r/2.
Wo mache ich den Fehler? Oder müsste es r in der Formel heißen?

 

[DanNHG]

Die Formel ist korrekt so,Hf ist 5

 

[luiseelli]

Bitte um Hilfe!
Irgendwie ist mir das Ergebnis der Formel unlogisch!
Hf=a*b/2r
wenn ich als Sehne 20 einsetze, a=b annehme und als Radius 10 ansetze bekomme ich 5 heraus.
Ich habe aber mal gelernt, das der Durchmesser die größte Sehne ist. Demnach müsste also das Ergebnis für meine Angenommenen Werte auf gehen, und Hf= r heraus kommen, und nicht r/2.
Wo mache ich den Fehler? Oder müsste es r in der Formel heißen?

Hallo ptl-bahn,

die Formel, die auf der Seite zu finden ist, ist eine Vereinfachung. In meiner Formelsammlung habe ich für den Segmentbogen folgende Formel:
r=(s/2)^2+h^2 / 2h ;
s ist Spannweite = Sehnenlänge = a+b
h ist Stichhöhe = Hf
Mit dieser Formel bekommst Du auch den korrekten Radius heraus. Diese Formel hat aber einen praktischen Nachteil: Die Stichhöhe h lässt sich nicht so einfach isolieren, da sie im Zähler als Summand auftritt. Ich denke, da das Verhältnis zwischen h und r im Gegensatz zu Deinem Beispiel in der Praxis des Eisenbahnbaus sehr klein ist, kann man die vereinfachte Formel gut verwenden. Mal ein Beispiel:
Bei s=20m und h=0,25m ist nach der genauen Formel der Radius r=200,08m, nach der vereinfachten Formel ist r=200m. Nun verändern wir h um einen cm auf h=0,24m. Wir erhalten einmal r=208,213.. und r=208,33... In der Praxis wird also die Herausforderung in der genauen Messung von h=Hf liegen, da dort die viel größere Fehlerquelle liegt, als in der etwas ungenauen Rechnung. Andersherum kann ich aber mal schnell ausrechnen, daß bei einem 10.000m-Halbmesser und 20m Sehnenlänge Hf=5mm sein müßte! Obwohl der tatsächliche Radius bei Hf=5mm natürlich 10.000,0025m beträgt. Ich hab schon immer geahnt, dass die bei der Bahn überhaupt nicht so genau arbeiten, wie sie immer tun

Achso, danke für die kleine Denkübung!

Thoralf

 

[Jan]

Das arbeiten mit "zugeschnittenen" Gleichungen war vor dem flächendeckenden auftreten elektronischer Rechenknechte gängige Praxis. Nicht nur bei der Bahn. Einfach mal in älteren technischen Lehrbüchern schmöckern.

 

[mswbahner]

Ich vermute, daß
r=(s/2)^2+h^2 / 2h
eigentlich r=[(s/2)^2+h^2] / 2h sein soll, wenn die Aussage mit dem schwierigen Isolieren von h gilt.
Auf beiden Seiten mit 2h multipliziert gibt
2rh=s²/4+h²,
dann 2rh auf beiden Seiten abziehen, so daß sich die Suche nach den Nullstellen einer gemischtquadratischen Gleichung ergib:
h²-2rh+s²/4=0
Hierauf die quadratische Ergänzung anwenden, und die beiden Ergebnisse sind:
h=r+Quadratwurzel[r²-s²/4] sowie h=r-Quadratwurzel[r²-s²/4]

Oder?
Gruß,

 

[jgifhorn]

Ja... stimmt. Die Vereinfachte Formel ist ungenau. Aber die Abweichung ist so gering, dass sie beim Vermessen keine Rolle spielt. Dort gelten mm. Bei Radien, die bei mehreren Hundert Metern liegen, bekommt man ne Abweichung die so gering ist, dass man sie kaum messen kann (1000stel mm).

Aber habt ihr ne Idee, wie das bei Übergangsbögen aussieht? Und was hast du für eine tolle Formelsammlung Thoralf? Die hätte ich auch gern...

 

[mswbahner]

@jgifhorn, das Thema hat einen gewissen Reiz - sage ich, der nicht unter Lösungsdruck steht. Ich hab keine Lösung, aber vielleicht ist ein Ansatzpunkt für dich dabei. Möglicherweise kaue ich dir schon hinlänglich Bekanntes wieder ...

Dieses bei Wikipedia haste sicher schon berücksichtigt?!
Allerdings hilft das noch nicht weiter, wenn die Bogenlänge zu gegebener Sekantenlänge unbekannt ist . Immerhin ließe sich die Kurve schon als Plot darstellen.

Der Abstand zwischen beiden Endpunkten des gewünschten Bogenstücks (der erste Punkt ist der Koordinatenursprung) ist gleich der vorgegebenen Sekantenlänge, und die ist nach Pythagoras gleich der Quadratwurzel aus der Summe der Endpunkt-x- und Endpunkt-y-Quadrate. Ein Programm, das x- und y-Koordinaten der Klothoide errechnet, ist am Bogenende angekommen, wenn eben diese Bedingung erfüllt ist.

Wenn du dieses Stück als zwischen Anfangs- und Endpunkt differenzierbaren Funktionsgraphen siehst, kannst du die Bogenlänge bestimmen (siehe hier, Abschnitt "Spezialfälle - Länge eines Funktionsgraphen"). Dafür wiederum brauchst du die Funktionsgleichung für das Bogenstück. Vielleicht hierüber, Unterpunkt "Berechnung der Krümmung für ebene Kurven, Fall 2" - umformen, integrieren ... An dieser Stelle hakt es bei mir leider: Die Krümmung ist bei der Klothoide in Abhängigkeit von der Bogenlänge gegeben

Hast du (wie auch immer ermittelt, vielleicht vom Rechenknecht interpoliert) f(x) für dein Bogenstück, dann ist der Abstand Sekantenmittelpunkt <-> Schnittpunkt mit der Orthogonalen durch die Sekantenmitte die gesuchte Pfeilhöhe. (Der Sekantenmittelpunkt hat die Koordinaten (x/2; y/2) mit x und y als Koordinaten des Bogenstückendpunkts, die Steigung der Orthogonalen ist der Kehrwert der Steigung der Sekante. Daraus die Funktionsgleichung der Orthogonalen ermitteln und mit f(x) gleichsetzen.)

 

[Stardampf]

Der Abstand zwischen beiden Endpunkten des gewünschten Bogenstücks (der erste Punkt ist der Koordinatenursprung) ist gleich der vorgegebenen Sekantenlänge, und die ist nach Pythagoras gleich der Quadratwurzel aus der Summe der Endpunkt-x- und Endpunkt-y-Quadrate. Ein Programm, das x- und y-Koordinaten der Klothoide errechnet, ist am Bogenende angekommen, wenn eben diese Bedingung erfüllt ist.
...
Hast du (wie auch immer ermittelt, vielleicht vom Rechenknecht interpoliert) f(x) für dein Bogenstück, dann ist der Abstand Sekantenmittelpunkt <-> Schnittpunkt mit der Orthogonalen durch die Sekantenmitte die gesuchte Pfeilhöhe.

Das trifft allerdings nur im Spezialfall Kreisbogen zu, nicht im Übergangsbogen!

Bezeichnen wir die drei Punkte im Gleisbogen von links nach rechts mit A, B und C, sowie den Schnittpunkt des Radius mit der Sehne als Punkt D. Weiterhin legen wir fest, daß die Krümmung im Übergangsbogen in Richtung A-C zunimmt, der Radius in dieser Richtung also kleiner wird.

Beim Kreisbogen ist die Tangente von Punkt B parallel zu der Sehne, welche sich aus der Verbindung der Punkte A und C ergibt. Der Radius im Punkt B halbiert den Winkel zwischen den Sehnen A-B und B-C und schneidet die Sehne A-C im rechten Winkel, die Strecken A-D und D-C sind gleich lang.

Im Übergangsbogen sind die Verhältnisse aufgrund der sich ändernden Krümmung etwas komplizierter:

Die Sehne A-C bildet mit der Tangente von Punkt B einen spitzen Winkel, der zur Tangente immer im rechten Winkel befindliche Berührungsradius schneidet also die Sehne A-C nicht im rechten Winkel und halbiert nicht den Winkel zwischen den Sehnen A-B und B-C. Die Strecken A-D und D-C sind ungleich lang. Da die sich ergebenden Dreiecke A-B-D und B-C-D somit nicht rechtwinklig sind, ist auch der Satz des Pythagoras nicht anwendbar.

Einen Lösungsansatz habe ich leider auch nicht...

 

[mswbahner]

Ausgehend von der Annahme, daß der Bogenanfang 1. im Koordinatenursprung liegt und 2. (für die Sekantenlänge unerheblich) die Tangente an den Bogen im Bogenanfang deckungsgleich mit der Abszisse ist:
"Der Pythagoras" für die Sekantenlänge gilt dort stets, egal, welche Windungen die Kurve (schwarz, blau, grün in Bild 1) bis zu ihrem Endpunkt vollführt.

Ist die Funktionsgleichung hinreichend genau bekannt - zur Not aus Streuplot extrapoliert -, die den Bogen beschreibt, so lassen sich alle beliebigen Pfeilhöhen errechnen: Ausgehend von einem frei gewählten Punkt auf der Sekante orthogonal auf den Bogen zielen. Die Funktionsgleichung der Sekante g(x) hätte die Steigung m=y/x (Koordinaten des Endpunkts Q) und den y-Achsen-Abschnitt b=0 (Ursprungsgerade). Jede Orthogonale dazu hätte die Steigung 1/m und liefe durch den frei gewählten Punkt auf der Sekante, von wo aus die Pfeilhöhe zu ermitteln wäre. Mit dieser Steigung und den Punktkoordinaten ergibt sich via Punkt-Steigungs-Form m=(y-y1)/(x-x1), aufgelöst nach y, die Funktionsgleichung h(x) der Geraden, auf der die gesuchte Pfeilhöhe liegt. Nun noch f(x) und h(x) gleichsetzen, so daß die Schnittstelle xs bekannt wird, ys dazu errechnen und zuletzt den Abstand Pfeilhöhenfußpunkt auf der Sekante zu Schnittpunkt h(x) mit f(x) ausrechnen - ebenfalls Pythagoras.
Bild 2 zeigt beispielhaft den Fall, daß die Pfeilhöhe auf der Sekantenmitte abgegriffen werden soll.


Es steht und fällt natürlich damit, daß der Verlauf des zu beurteilenden Bogenstücks hinlänglich genau als Funktionsgleichung beschrieben wird.

 

[Stardampf]

Ausgehend von der Annahme, daß der Bogenanfang 1. im Koordinatenursprung liegt und 2. (für die Sekantenlänge unerheblich) die Tangente an den Bogen im Bogenanfang deckungsgleich mit der Abszisse ist:

Für die Gesamtlänge der Sehne gilt freilich der Pythagoras.
Die wichtige Tangente kann aber nicht Deckungsgleich mit der Abszisse sein, da sie den Bogen ncht im Koordinatenursprung tangiert, sondern in Deiner zweiten Skizze den mit Mp bezeichneten Punkt. Fällt man von diesem Punkt ein Lot über der Tangente, hat man die Gerade, auf welcher der Radius abgetragen werden muß. Diese Gerade ist aber nur im Kreisbogen rechtwinklig zu der von ihr geschnittenen Sehne, da nur dort die Sehne zur Tangente an Mp parallel ist. Bei einem Bogen mit sich stetig verringerndem Radius wird die Sehne vom Radius schiefwinklig und außermittig geschnitten und damit der Pythagoras an dieser Stelle ungültig, da die entstehenden Dreiecke nicht rechtwinklig sind.

Die Kreistangente trifft den Kreis also in genau einem Punkt. Sie steht dort senkrecht auf dem zu diesem Punkt gehörenden Berührungsradius.

Auch im allgemeinen Fall steht die Tangente senkrecht auf dem zum Berührungspunkt gehörenden Radius des Krümmungskreises, sofern dieser existiert.

Wikipedia: Tangente

Der Fehler ist, Daß Du den Radius rechtwinklig auf die Sehne setzt, anstatt rechtwinklig zur Tangente des Punktes auf der Kurve, der zu P und Q den gleichen Abstand hat.

 

[mswbahner]

Stardampf,
völlig richtig. Allerdings spezifizierte ich, es sei die "Tangente an den Bogen im Bogenanfang" deckungsgleich mit der Abszisse. Ich richte mein Bezugssystem genau so aus, daß das gegeben ist. Alle anderen Myriaden von Tangenten an dieses Bogenstück sind es dann bei Krümmung ohne Wendepunkt zwischendrin natürlich nicht, auch nicht die in MP.

jgifhorn schrieb in seinem Eingangspost von Vermessung:

[...] nicht nur mit der Entwicklung einer Gleistrasse beschäftigt, sondern auch mit deren Vermessung? [...]

Ich gehe davon aus, daß das Gleis in natura schon daliegt. Nun wird die Gleislage mit Planunterlagen verglichen. Von einem Gleis-Fixpunkt abc ausgehend kann ich dann das von jgifhorn wohl noch zu schreibende Programm starten: "Fixpunkt abc ist der 1. Auflagepunkt meiner 16-m-Meßlatte (der Sekante)". Hierher legt das Programm den Koordinaten-Ursprung und spuckt mir nach Sollvorgabe aus: "Pack die 16-m-Latte auf die Schiene, hier müßte im weiteren Verlauf ein Linksbogen vorliegen, die Latte hängt also links über, und die Schiene sollte sich rechts von der Latte in verschiedenen Abständen nach Planvorgabe wiederfinden." Das Programm hat den Kurvenverlauf nach Planvorgabe seit Fixpunkt abc als Daten vorliegen. Es spuckt nun aus: "Miß bei den Lattenlängen 1 m, 2 m, ..., 15 m nach rechts den Abstand Latte - Schiene; die Schiene müßte nach Plan 2 cm, 3 cm, ..., 2 cm weit entfernt sein." Das tut der Meßtrupp brav und dokumentiert seine Ergebnisse.
Und nach mehreren einander vielfach überlappenden Meßdurchgängen im weiteren Gleisverlauf kann es losgehen: Es werden Abweichungen vom Soll festgestellt, und so werden Gleise gerückt, bis die Maße stimmen. Und wenn die Maße (dann) stimmen, stimmen automatisch die vorgesehenen Radien in den einzeln Punkten.
Oder das Programm interpoliert den Ist-Gleisverlauf seit Fixpunkt abc aus den aufgenommenen Ist-Pfeilhöhen (macht eine Funktionsgleichung für den betrachteten Bogen daraus) und kann schließlich die Ist-Radien in jedem Punkt locker errechnen, zum Beispiel eben hiermit: Unterpunkt "Berechnung der Krümmung für ebene Kurven, Fall 2

Der Meßtrupp muß sich nicht mit Differentialrechnung und Geometrie plagen, sondern fährt sich heißen Tee aus der Thermoskanne nebst Leberwurst-Rosinenbrot ein und freut sich auf den Feierabend.

 

[Stardampf]

Leberwurschtbrötchen und Abszisse, alles Pillepalle, solange der Fehler im Prinzip steckt.

Die einzgen rechten Winkel hier sind am Koordinatensystem und zwischen Radius und Tangente.
Auch die Sehne wird vom Radius nicht in der Mitte geschnitten und schon garnicht im rechten Winkel.

 

[mswbahner]

Och Mönsch Stardampf, du weißt doch: Es gibt an jeder Kurve unendlich viele Tangenten! Darauf beruht die gesamte Infinitesimalrechnung ...

Dem, was du da skizziert hast, stimme ich zu. Ich behaupte nirgends, die Orthogonale zur Sekante h(x) durch M und MP, die ich in grün in meine vorige Skizze eingezeichnet habe, sei eine Senkrechte auf die Tangente an die Kurve in MP, denn das wäre sie nur, wie du unterstreichst, wenn wir es mit einem Kreisbogen zu tun hätten (gleiche Krümmung, ergo gleicher Radius zum Kreisbogen).

Entlang der Sekante kann ich so viele Pfeilhöhen (edit mswbahner 22:12 am 02.08.11: Es gibt offensichtlich nur eine "Pfeilhöhe" (siehe Link), ich habe den Begriff bisher falsch verwendet, und zwar im Sinne von "Abstand der Kurve von der Sekante von beliebigem Sekantenpunkt aus betrachtet." Hatte mich von der globalen Verwendung des Begriffs auf der Seite der Gleisbau-Welt, erste Skizze auf dieser Seite, irreleiten lassen.), wie ich eben lustig bin, auf den Bogen ziehen. Und in zufällig vielleicht mal einem Fall liegt dieser Abstand auch in Linie mit dem Radius an die Kurve in genau diesem einen Punkt.

Die Sekante ist eine Standlinie, von der aus im rechten Winkel auf die zu vermessende Kurve gezielt wird (mit den Abständen): rechtwinklig zur Standlinie, nicht rechtwinklig zur Kurve! Aus den Koordinaten der Endpunkte der Sekante kann man die Funktionsgleichung der Sekante ermitteln. Wenn man nächstens die Koordinaten der Punkte F1, F2, F3, ... festlegt, von wo aus die Abstände PH1, PH2, PH3, ... auf die Kurve geschossen werden - diese Punkte liegen zwingend auf der Sekante -, kann man damit und mit dem Fakt, daß die Abstände senkrecht zur Sekante sind, sofort die Funktionsgleichungen der Geraden errechnen, auf denen die Abstände liegen. UND NEIN, diese Geraden sind in der Regel nicht die Radien an die Kurve, wenn kein Kreisbogen vorliegt. Die Radien liegen irgendwie schiefwinklig - wie du es skizziert hast - zu diesen Abständen. Daß ich das wohl weiß, sollen die von mir eingezeichneten Tangenten t1, t2, t3 an die Kurve in den Punkten B1, B2, B3 dokumentieren. Senkrecht zu diesen Tangenten t1, t2, t3 liegen die Radien. Die sind jedoch überhaupt nicht von Belang, weil sich der Radius von Kurvenpunkt zu Kurvenpunkt verändert. Will jemand unbedingt die Radien zu jedem einzelnen Kurvenpunkt haben, braucht er nur die Kurvenfunktionsgleichung zweimal abzuleiten, dann die Formel für die Krümmung zu nehmen, die ich zweimal verlinkt habe, und von der ermittelten Krümmung den Kehrwert zu nehmen: *zack*, da ist der Radius in einem einzelnen Punkt der Kurve.

Setzt man nun jede der Funktionsgleichungen zu allen Abständen mit der Kurvengleichung gleich, kann man den Schnittpunkt "Gerade durch Abstand" mit "Kurve" errechnen. Damit kenne ich alle Pärchen F1-B1, F2-B2, F3-B3, ... mit ihren Koordinaten. Und hier kommt wieder Herr Pythagoras zum Zuge, um den Abstand zwischen F und B zu ermitteln, der beträgt immer noch die Quadratwurzel aus der Summe von Differenz der x-Koordinaten und Differenz der y-Koordinaten.


Noch ein Nachtrag gegen 23 Uhr:
Wenn es darum ginge, den größten Abstand der Kurve von der gewählten Sekante zu ermitteln, braucht man nur die erste Ableitung der Kurvengleichung des betrachteten Intervalls. An der Stelle, an der die Kurve dieselbe Steigung wie die Sekante hat (f'(x)=m), ist der Abstand "Kurve zu Sekante" am größten. In beigefügtem Bild 3 ist dann die Strecke F-B die Pfeilhöhe und wieder über Pythagoras errechenbar.

 

[Per]

Tachymeter

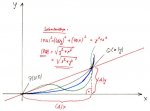
Ist es heutzutage nicht einfacher, die Koordinaten zu überprüfen (zur Not mit Tachymeter , die können auch Messungen direkt in den Kompjuter übertragen) als die Pfeilhöhen zu messen (und wie wir sehen zu berechnen)?


DIE kenne ich noch aus meiner Jugend